LU Decomposition
LU分解
LU分解是矩阵分解的一种,将矩阵A分解成下三角矩阵L和上三角矩阵U即 A = L * U;LU分解主要用于求解线性方程组、求逆矩阵或计算行列式中;
LU分解的原理
首先通过高斯消元将矩阵A变成上三角矩阵(主对角线下的元素全为0),这个上三角矩阵就是U,假设A是一个三阶的方阵,通过左乘一个消元矩阵就可以变成U
- (E33E31E21)A = U
- A = (E33E31E21)-1 * U
这个消元矩阵的逆就是L,对消元矩阵的解释可以参考(https://www.cnblogs.com/Dumblidor/p/5751579.html)
杜尔里特算法(Doolittle algorithm)
前面我们已经有 A = L * U 的公式,即
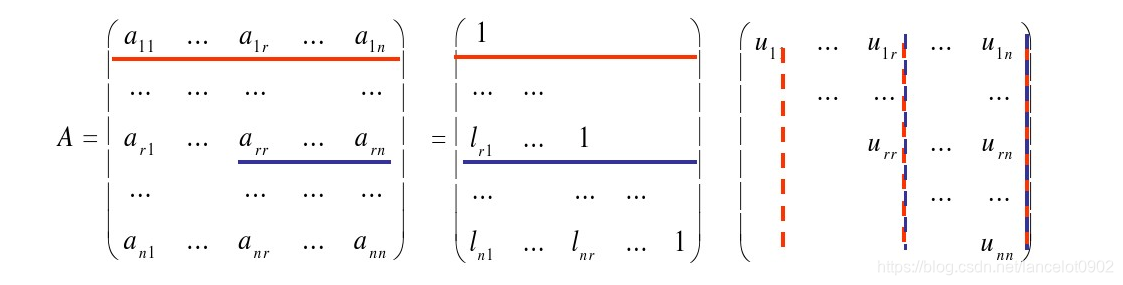
我们可以用矩阵乘法推到出LU分解的计算公式,根据矩阵乘法公式
- A的第一行,A1k = U1k
- A的第r行(r=[1,n])主对角线右侧元素arj
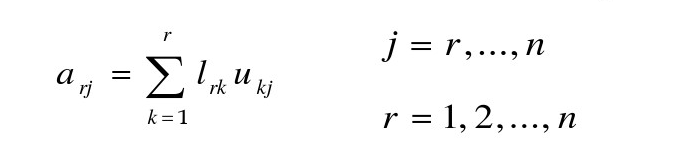
同理,可以推导出第r行主对角线以下的元素air
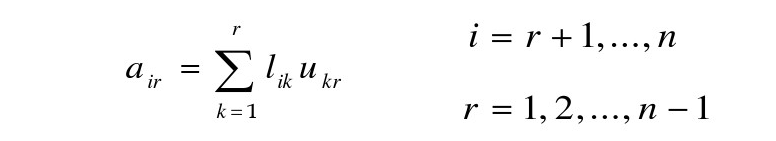
综上,可以得到


上述的过程就是A的Doolittle分解
