Gauss Jordan（3）

先看一个高斯消元求逆的例子

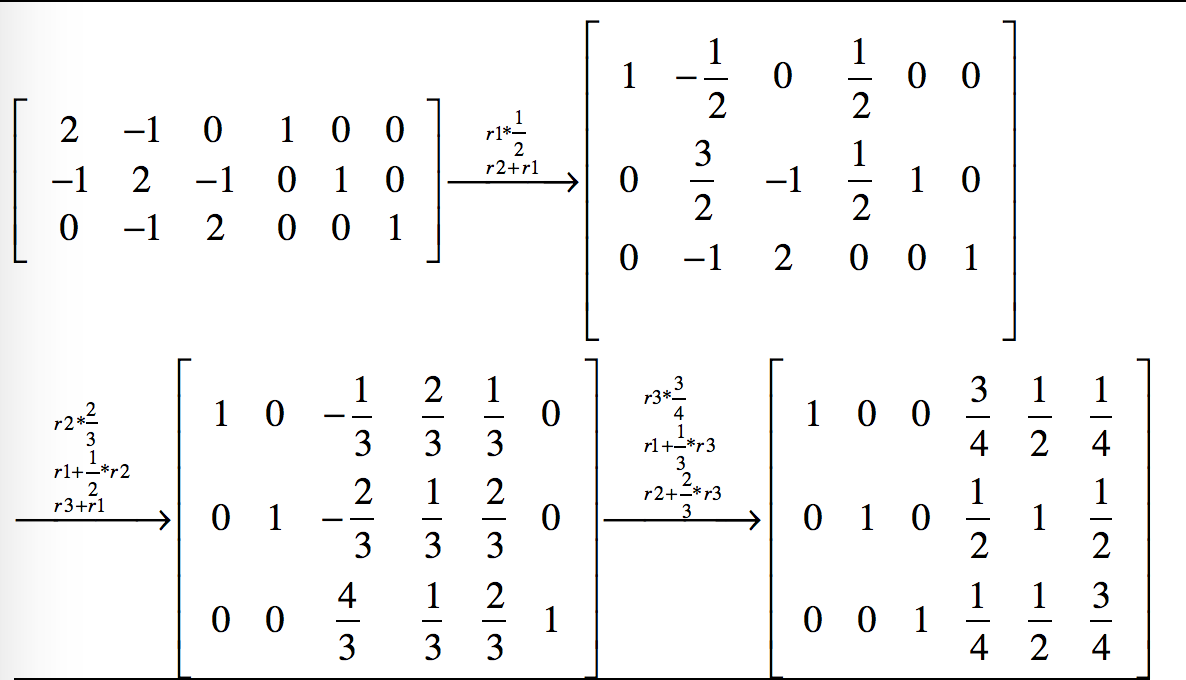
观察上面增广矩阵的变化过程，我们发现在每一步迭代的结果中，增广矩阵左侧有x列已化为单位矩阵时，右侧就有n-x列保持着单矩阵的样子，即总能从增广矩阵中抽出n列组成一个单矩阵。同时左侧已化为单位矩阵的那几列在以后的行初等变换为始终保持不变

这也就意味着我们可以把右侧不再是单位矩阵的放到左侧刚变成单位阵的那一列，这样就可以省下一半的空间；为什么可以这么做？

举个例子，当我们处理第一列的时候要把第一列化成1,0,0这样的单位矩阵的形式，处理完后第一列将会一直保持这个形式不会再变化，所以可以将它抛弃，以右侧对应列（初等行变换后的右侧第一列）替换，因为右侧矩阵是要得到的逆矩阵，正好替换到左侧矩阵对应列，在之后的步骤中随着其它列进行初等行变换就可以了，最后的结果就是要得到的逆矩阵

以上想法能成立的原因是在将左侧第x列化成单位阵得到时候，在右侧矩阵第x列的右侧几列一直保持单位阵不变，所以不需要额外的空间去记录，也就是说上面那个输入矩阵A在高斯消元时不需要进行和行间的互换（也就是说每一列的主元都在主对角线上）

再看一个例子，输入矩阵A为

1
2
3

0  1  2 | 1  0  0
1  1  4 | 0  1  0
2 -1  0 | 0  0  1

用按列选主元的gauss处理A得到第一列时，要将第三行和第一行互换

1
2
3

2 -1  0 | 0  0  1
1  1  4 | 0  1  0
0  1  2 | 1  0  0

这时右边矩阵变了，不再是单位阵了，继续处理第一列变成

1
2
3

1 -0.5  0 | 0  0  0.5
0  1.5  4 | 0  1 -0.5
0    1  2 | 1  0    0

再观察上面的矩阵就发现右侧矩阵不再保持单位矩阵的形式，也就是说右侧矩阵的变换不能被舍弃，所以对于有行交换操作的矩阵上述算法不再适用，所以需要改进算法

进行交换的目的是将这列的最大值放到主对角线上，我们可以不用交换，我们可以该列在主对角线上的元素所在行乘上一个系数，让这个元素扩大几倍，这样我们可以不用交换，就可以保持右边矩阵的n-x列为单位阵了，这样就可以把高斯约旦消元空间的消耗控制在n*n了