Gauss Jordan(1)
Gauss Jordan法求逆矩阵
Gauss Jordan消元法是高斯消元法另一个版本,与高斯消元不同的是,高斯消元将矩阵化成上三角矩阵,G-J消元把矩阵化成单位矩阵;与高斯消元相同的是都是用来求解线性方程组的解
Gauss Jordan法介绍
当要求矩阵A的逆时,在A的右边放一个单位矩阵I,[A | I]就是增广矩阵,对A加减消元时,同样的步骤也作用于I上,当将A变成单位矩阵后,I就变成了P(A的逆),即[I | P]
G-J消元法就是通过一系列的初等行变换将[A | I]变成[I | P]的形式
如图
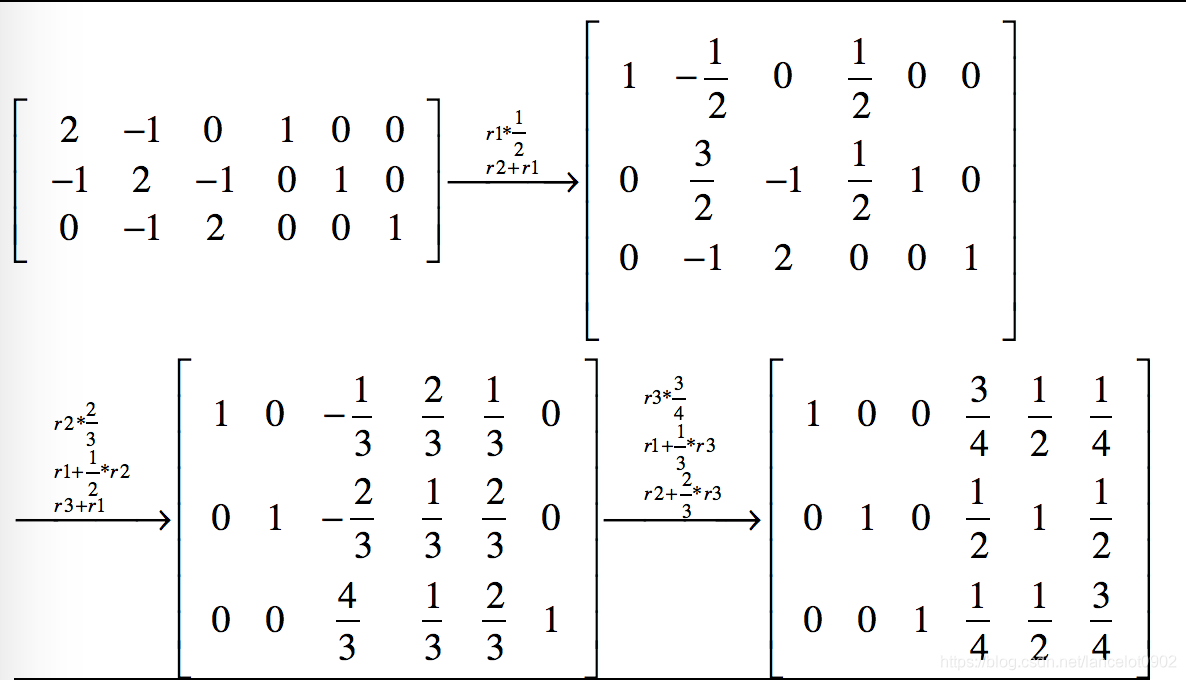
选取主元的Gauss Jordan
数值计算的迭代过程往往都伴随着舍入误差的累积,所以最终的结果也会有误差,如果这个最终的误差在一个可控的范围内,则称该算法为数值稳定的算法,否则为数值不稳定的算法。什么时候会造成数值不稳定?比如算法某一步要除以一个很小的数,小到绝对值趋近于0,商趋于无穷大,此时舍入误差大到不可控。相对于除以一个很小的数,除以一个很大数是比较安全的,因为真实的商值本来就趋于0,舍入后取0,这个误差并不大。所以G-J消元法有一种“稳定”的形式,即选取主元的G-J消元法
选主元的方法
- 在每一个循环过程中,先找到绝对值最大的那个元素
- 然后通过行变换将那个元素移动到主对角线的位置上
- 然后将主元所在的行除以主元,将主元变成1,然后通过加减消元变换将主元所在的行列变成单位矩阵的形式
- 在下一个循环过程中不考虑上一个主元所在的行列,在其它范围寻找下一个主元
选主元的方法虽然使算法比较稳定,但同时也增加了计算量,一种折中的方法“选取列主元”
选取列主元的方式是在第i次循环迭代中,从第i列中选主元,同样第i列中第i行之前的元素不在候选的范围内
假如矩阵是n阶矩阵,那么在每一次循环中对矩阵中的每一个元素都要处理,所以时间复杂度是n3
参考:
